图解Transoformer学习 (Attention Mechanism)
[!NOTE] Title
文章内容来自于 Illustrated Transformer
总览
我们从高层次总览一下, Transformer是什么?

image.png
其实深入到内部的话其实构造就很简单.

image.png
就是一堆编码器和一堆解码器.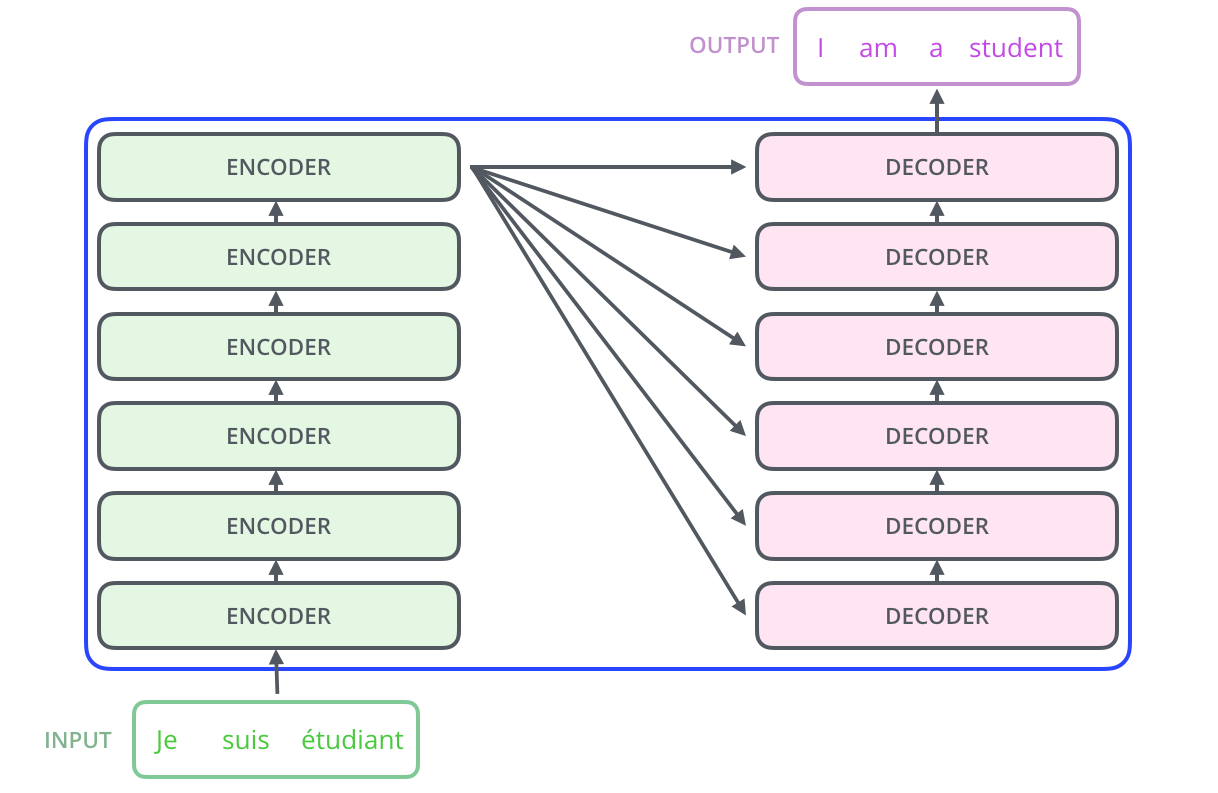
image.png
在深入到Encoder 内部的话.就是两个子层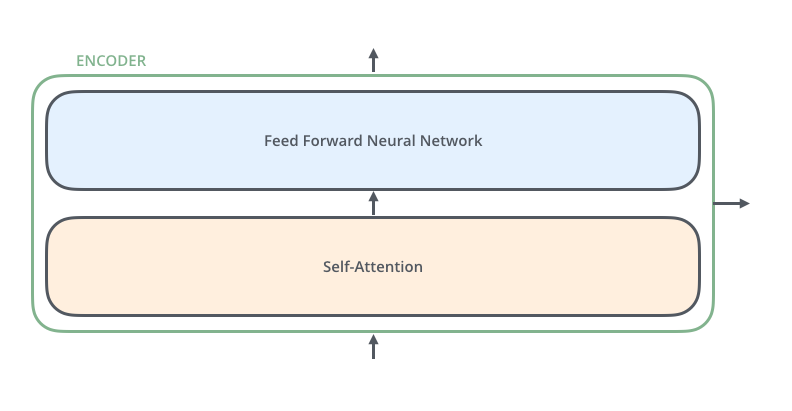
image.png
- 编码器的输入首先通过一个自注意力层——这个层帮助编码器在编码特定单词时查看输入句子中的其他单词。
- 自注意力层的输出被输入到一个前馈神经网络。完全相同的神经网络独立应用于每个位置。
让我们再看下Decoder内部结构.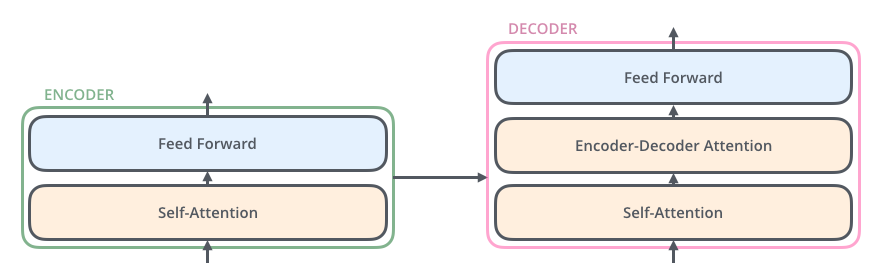
image.png
解码器也具有这两层,但它们之间有一个注意力层,有助于解码器关注输入句子的相关部分.
Tensor (张量) Input
现在我们已经看到了模型的各个主要组件,让我们开始研究各种向量/张量,以及它们如何在这些组件之间流动,将训练模型的输入转换为输出。
在自然语言处理应用中,我们首先使用嵌入算法将每个输入词转换为向量。

每个词嵌入到大小为 512 的向量中。我们将用这些简单的方框来表示这些向量。
嵌入只发生在最底层的编码器中。所有编码器共有的抽象是它们接收一个大小为 512 的向量列表——在最底层的编码器中,这将是词嵌入,但在其他编码器中,它将是直接位于其下方的编码器的输出。这个列表的大小是一个我们可以设置的超参数——基本上它将是我们的训练数据集中最长句子的长度。
让我们看下Tensor输入到Encoder中发生了什么?
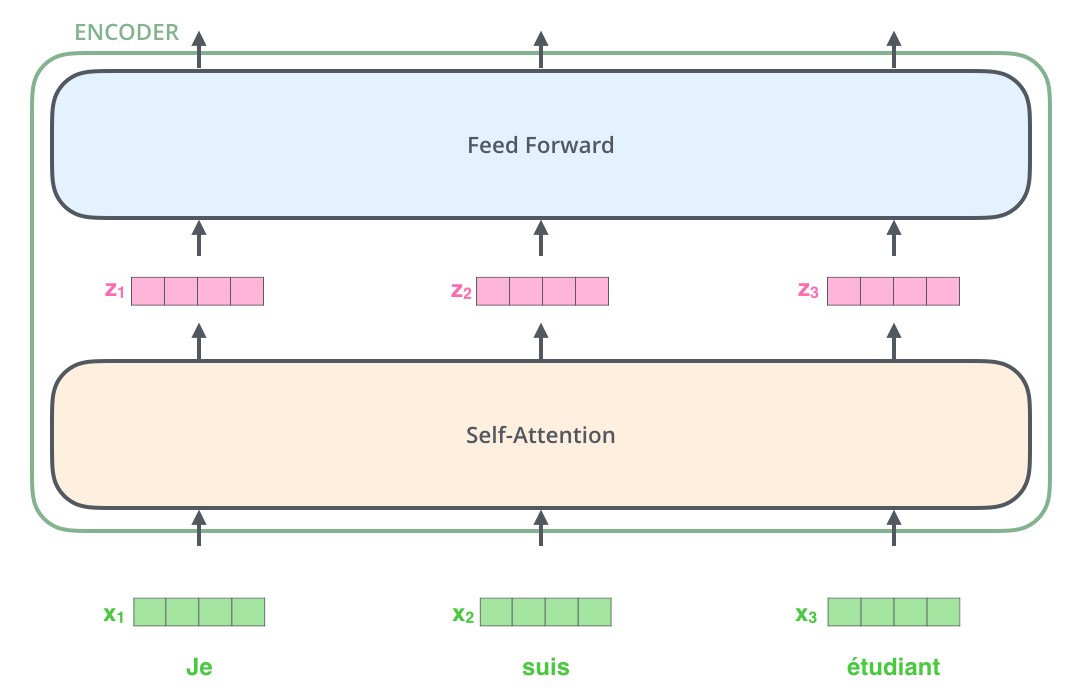
image.png
这里我们开始看到 Transformer 的一个关键特性,即每个位置的词在编码器中通过自己的路径流动。在这些路径之间存在自注意力层的依赖关系。然而,前馈层没有这些依赖关系,因此各种路径可以在通过前馈层时并行执行。
我们用一个更简单的语句来展示这个过程.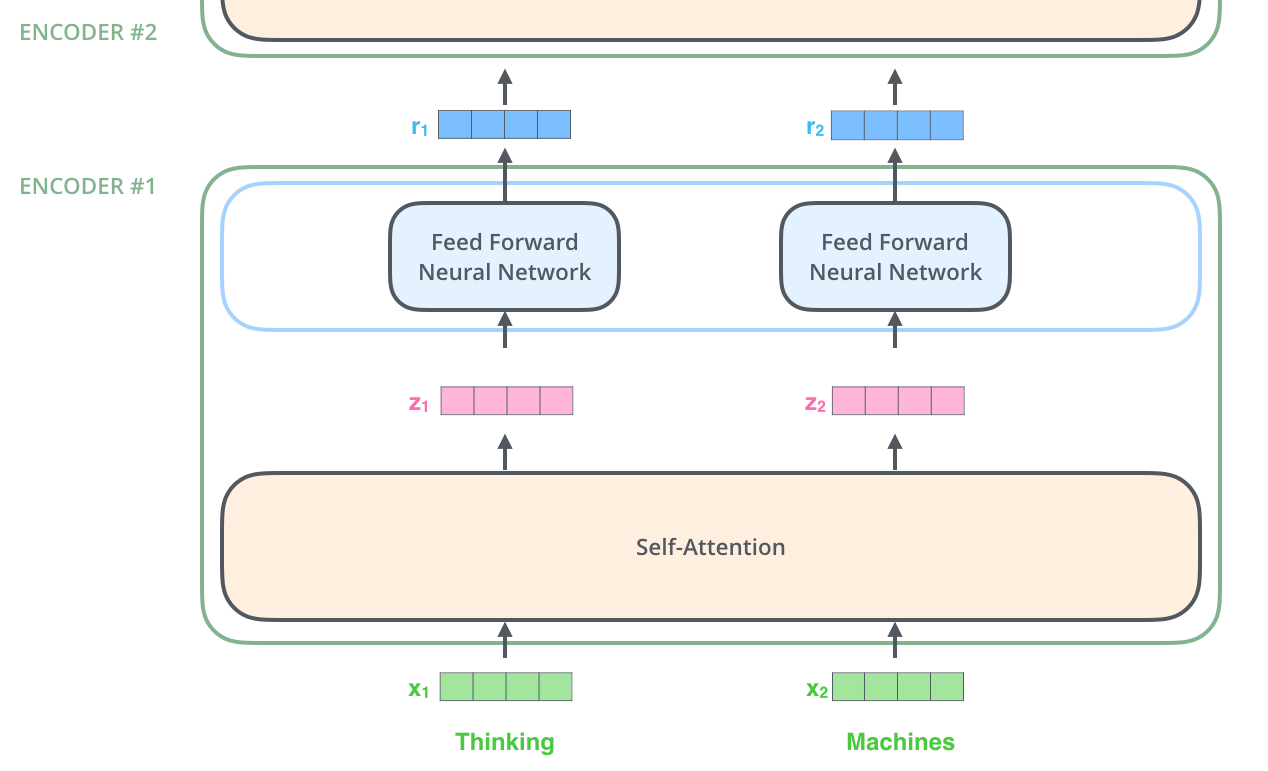
The word at each position passes through a self-attention process. Then, they each pass through a feed-forward neural network -- the exact same network with each vector flowing through it separately.
Self-Attention总览
让我们来提炼一下Self-Attention是如何工作的?
以下句子是我们想要翻译的:"The animal didn't cross the street because it was too tired, The animal didn't cross the street because it was too tired
这句话中的“it”指的是什么?是指街道还是动物?这对人类来说是一个简单的问题,但对算法来说并不简单。
当模型处理单词“it”时,自注意力使其能够将“it”与“animal”关联起来。
用图示展示的话, 就能发现在当前Attention机制下, it 和 the animal关联都最高
随着我们在编码器#5(堆栈中最顶层的编码器)中编码单词"it",注意力机制的一部分专注于"The Animal",并将它的一部分表示编码进"it"的编码中。
详解 Self-Attention
首先,我们来了解一下如何使用向量计算自注意力,然后继续探讨其实际实现——使用矩阵计算。
第一步 Query向量Key向量Value向量
计算自注意力机制的第一步是从编码器的每个输入向量中创建三个向量(在这种情况下,每个词的嵌入)。因此,对于每个词,我们创建一个Query向量、一个Key向量和一个Value向量。这些向量是通过将嵌入乘以我们在训练过程中训练的三个矩阵来创建的。
注意,这些新向量在维度上小于嵌入向量。它们的维度是 64,而嵌入和编码器输入/输出向量的维度是 512。它们不必更小,这是为了使多头注意力的计算(主要是)保持常数而做出的架构选择。
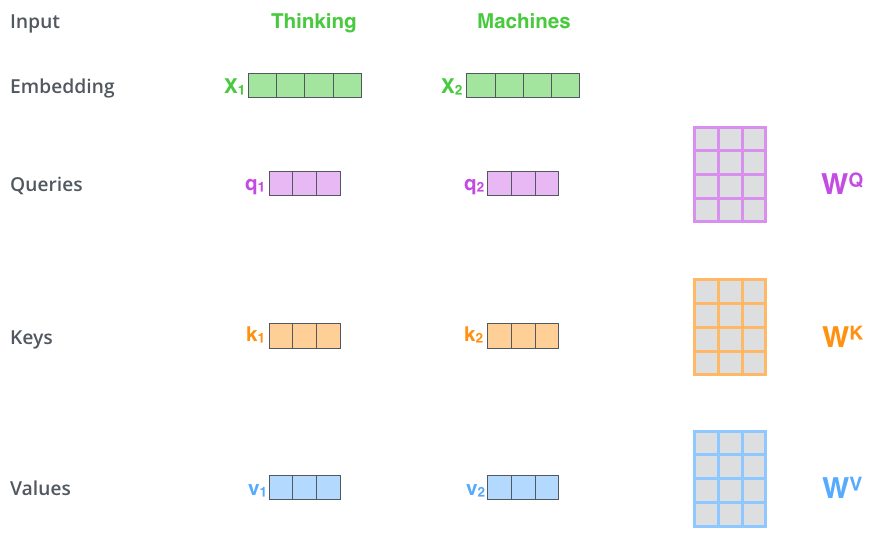
将 x1 乘以 WQ 权重矩阵得到 q1,这是与该单词关联的“Query”向量。我们最终为输入句子中的每个单词创建一个“Query”、“Key”和“Value”投影。
什么是“Query”、“Key”和“Value”向量?
这些是用于计算和思考注意力的抽象概念。一旦你阅读以下关于注意力如何计算的内容,你将大致了解每个这些向量所扮演的角色。
第二步 计算Score
计算自注意力步骤的第二步是计算一个分数。比如说,我们正在计算这个例子中第一个词“Thinking”的自注意力。我们需要将输入句子中的每个词与这个词进行评分。这个分数决定了我们在编码某个位置的词时,对输入句子其他部分的关注程度。
Score是通过将查询向量与我们要评分的单词的关键向量进行点积来计算的。所以如果我们正在处理位置#1 的单词的自注意力,第一个得分将是 q1 和 k1 的点积。第二个得分将是 q1 和 k2 的点积。
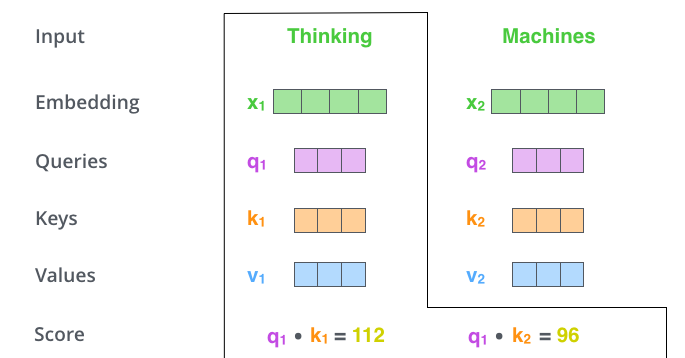
image.png
第三步第四步 归一化
将SCore除以 8(论文中使用的键向量的维度的平方根 - 64。这导致具有更稳定的梯度。这里可能有其他可能的值,但这是默认值),然后将结果通过 softmax 操作。Softmax 将分数归一化,使它们都为正且总和为 1。
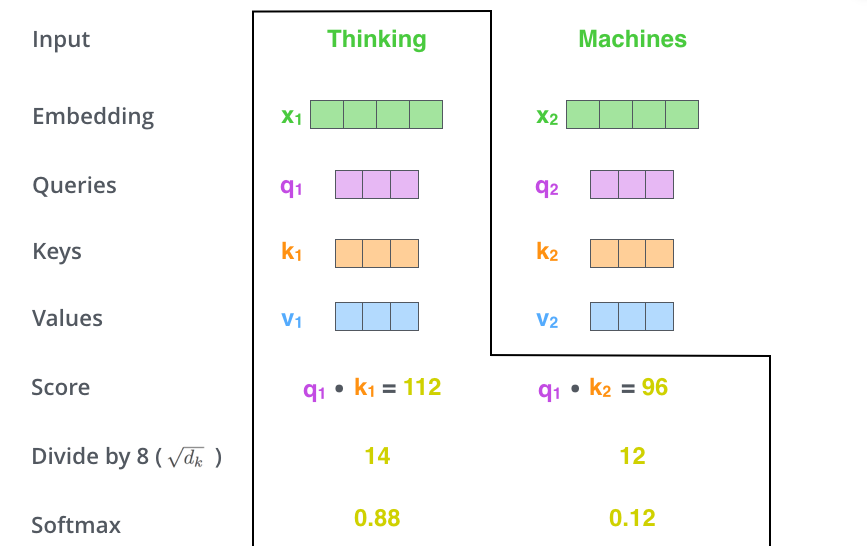
image.png
这个 softmax 分数决定了每个词在这个位置的表达程度。显然,这个位置的词将具有最高的 softmax 分数,但有时关注与当前词相关的另一个词是有用的。
第五步 向量处理
将每个Value向量乘以 softmax 分数(为求和做准备)。这里的直觉是保持我们想要关注的单词的值不变,并通过将它们乘以微小的数字(例如 0.001)来淹没无关的单词。
第六步 加权值向量的和
第六步是求加权值向量的和。这产生了当前位置(对于第一个词)的自注意力层的输出。
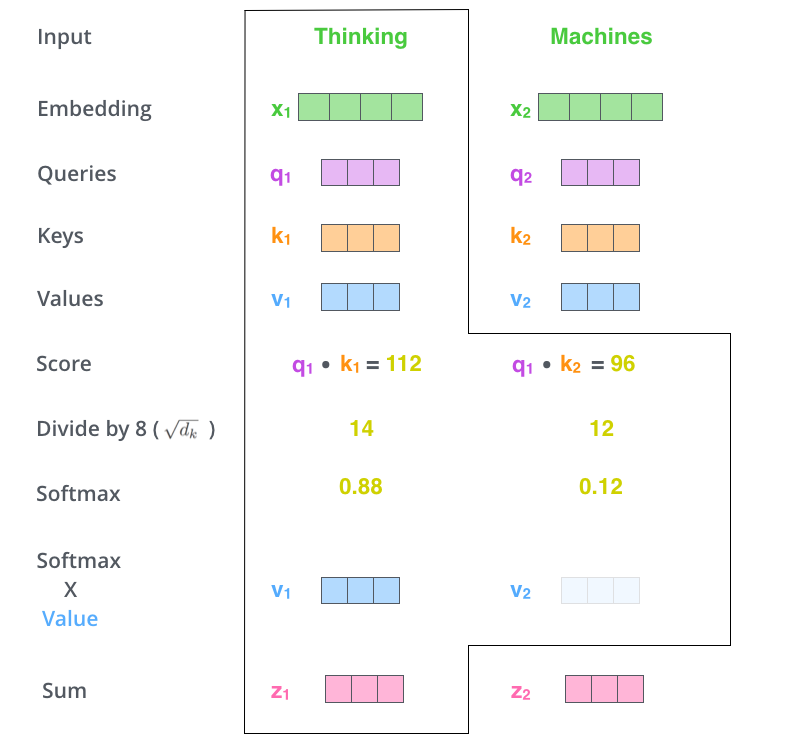
image.png
这标志着自注意力计算的结束。得到的向量是我们可以发送到前馈神经网络的一个。然而,在实际实现中,这个计算以矩阵形式进行,以便更快地处理。既然我们已经看到了在词级别上的计算直觉,现在让我们看看这一点。
Self-Attention 矩阵计算
第一步 映射矩阵
第一步是计算查询(Query)、键(Key)和值(Value)矩阵。我们通过将嵌入打包到矩阵 X 中,然后乘以我们训练的权重矩阵(WQ、WK、WV)来实现这一点。
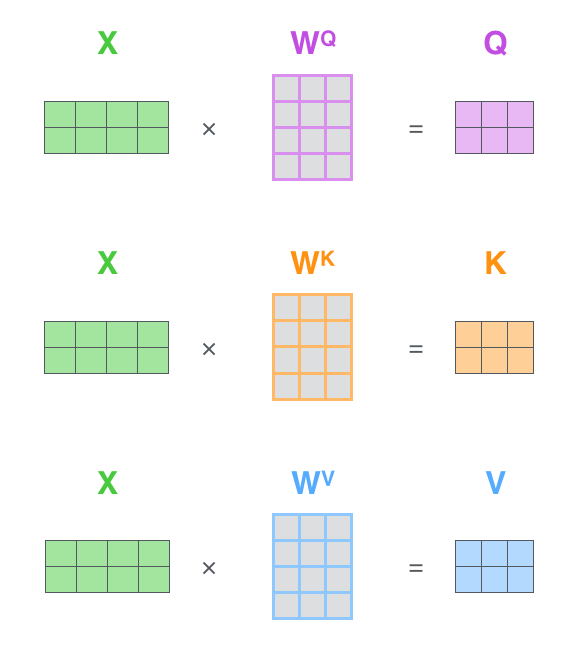
X 矩阵中的每一行对应输入句子中的一个单词。我们再次看到嵌入向量的大小差异(512,或图中的 4 个框),以及 q/k/v 向量(64,或图中的 3 个框)
第二步 计算
由于我们处理的是矩阵,我们可以将之前步骤二至六合并为一个公式来计算自注意力层的输出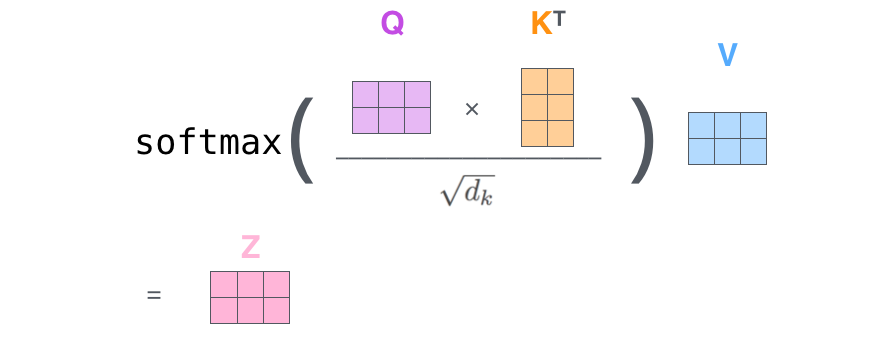
image.png
Multi-head Attention
多头注意力机制是为了优化自注意力机制的表现.
- 它扩展了模型关注不同位置的能力。
在上面的例子中,z1 包含了一些其他编码,但它可能被实际单词本身所主导。如果我们正在翻译像“动物没有过马路,因为它太累了”这样的句子,知道“它”指的是哪个单词将是有用的。
- 它为注意力层提供了多个“表示子空间”。
正如我们接下来将看到的,在多头注意力中,我们不仅有单一的,而是有多个查询/键/值权重矩阵集(Transformer 使用八个注意力头,因此每个编码器/解码器最终有八个集合)。这些集合中的每一个都是随机初始化的。然后,在训练之后,每个集合都用于将输入嵌入(或来自较低编码器/解码器的向量)投影到不同的表示子空间中。
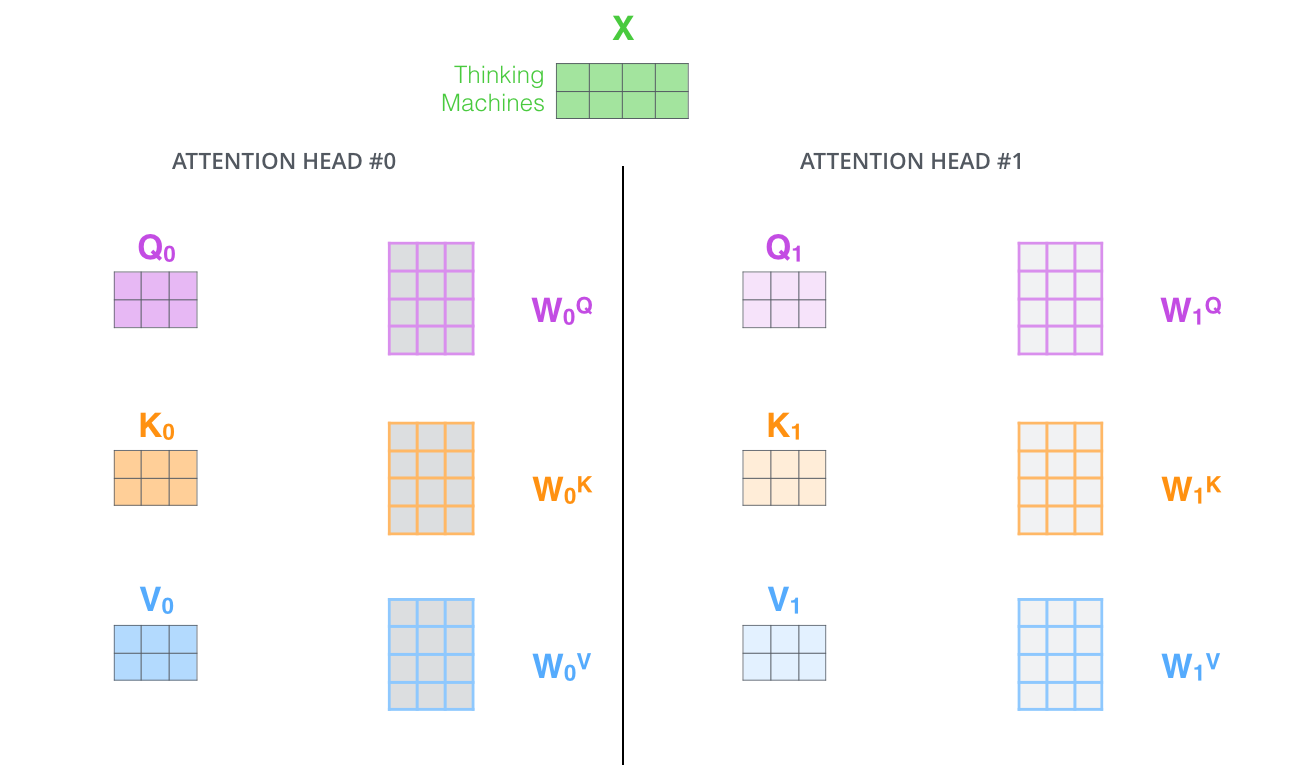
使用多头注意力机制,我们为每个头维护独立的 Q/K/V 权重矩阵,从而得到不同的 Q/K/V 矩阵。与我们之前做的一样,我们将 X 乘以 WQ/WK/WV 矩阵以产生 Q/K/V 矩阵。
如果我们进行上述相同的自注意力计算,只是每次使用不同的权重矩阵,总共进行八次,最终得到八个不同的 Z 矩阵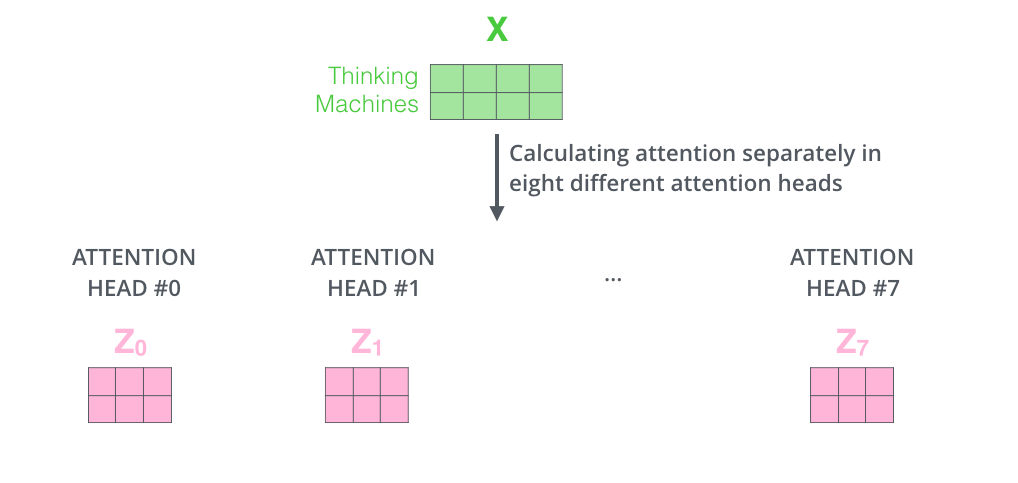
image.png
Feed-froward layer challenge
这给我们带来了一些挑战。前馈层不期望有八个矩阵——它期望一个单一的矩阵(每个词一个向量)。因此,我们需要一种方法将这些八个矩阵压缩成一个单一的矩阵。
我们将矩阵连接起来,然后乘以额外的权重矩阵 WO。
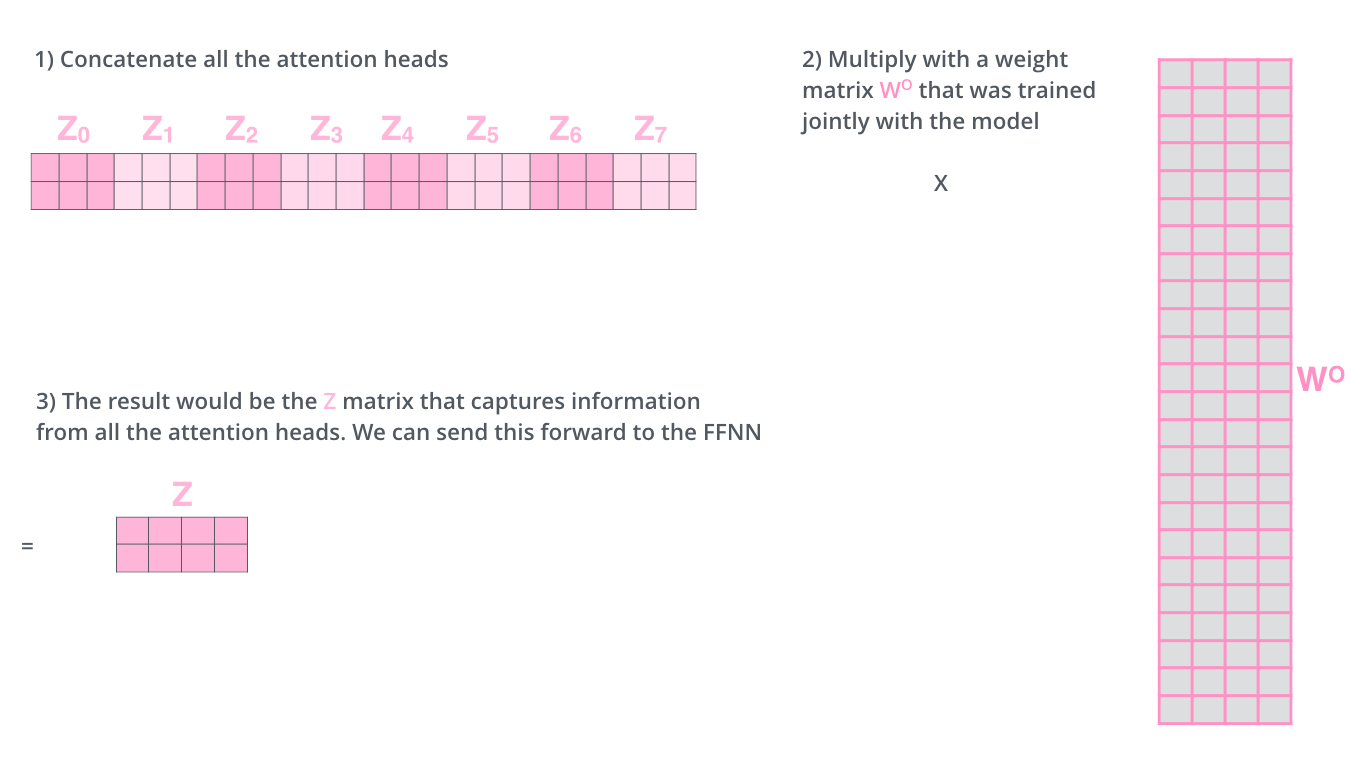
image.png
这基本上就是多头自注意力机制的全部内容。我意识到这涉及到很多矩阵。让我尝试将它们全部放在一个视觉图中,这样我们就可以在一个地方查看它们。
All steps
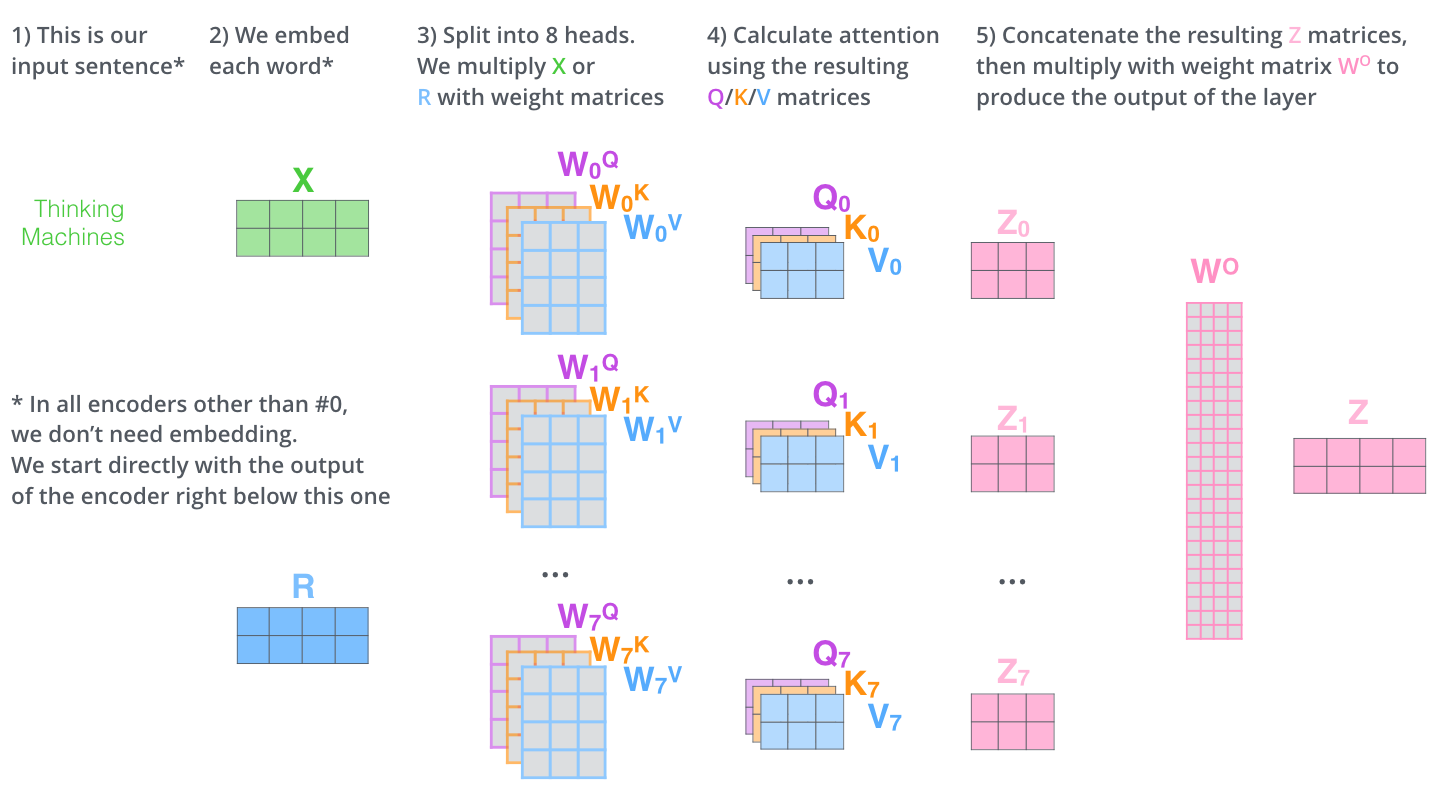
image.png
再通过图示来回顾之前的例子. 看看不同的注意力头在编码我们例子中的单词“it”时关注在哪里?
随着我们对单词"it"进行编码,一个注意力头主要关注"the animal",而另一个则关注"tired"——从某种意义上说,模型对单词"it"的表示融合了"animal"和"tired"的一些表示。
如果我们把所有的注意力头加到图片上,然而,事情可能更难解释.
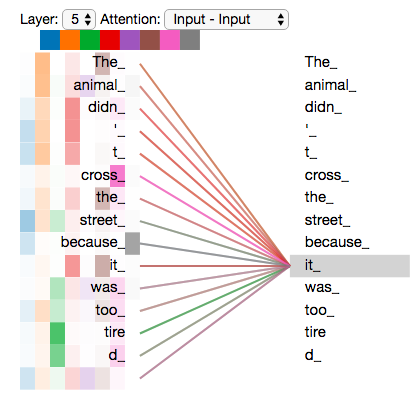
image.png
Representing The Order of The Sequence Using Positional Encoding(使用位置编码表示序列的顺序)
模型中目前所描述的缺失之处是,没有一种方法来考虑输入序列中单词的顺序。
为了解决这个问题,Transformer 为每个输入嵌入添加一个向量。这些向量遵循模型学习到的特定模式,有助于确定每个词的位置,或者序列中不同词之间的距离。
这里的直觉是,将这些值添加到Embedding中,一旦它们被投影到 Q/K/V 向量并在点积注意力期间,就能提供embedding向量之间的有意义的距离。
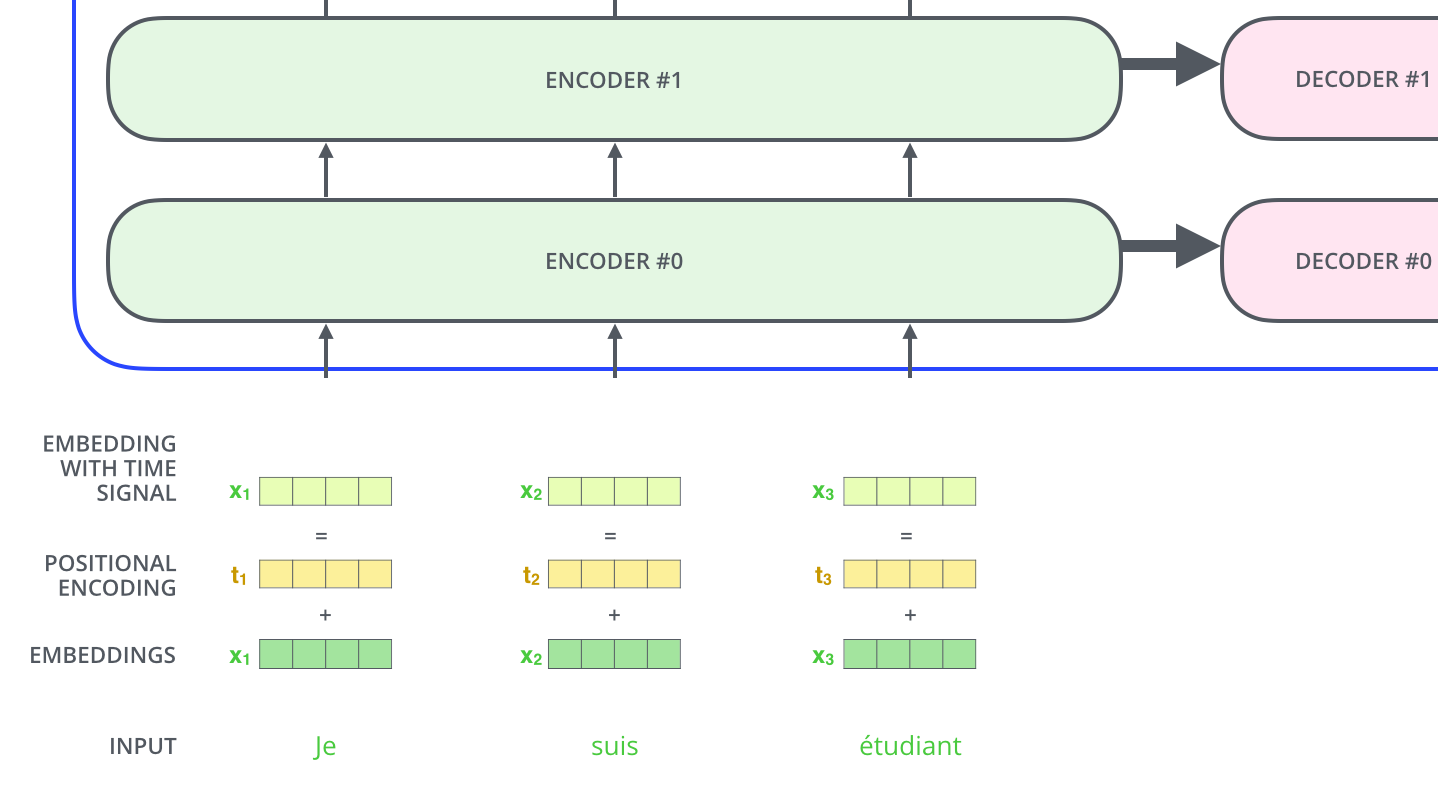
为了给模型一个词语顺序的感觉,我们添加位置编码向量——其值遵循特定的模式。
输入向量X1 与 位置编码 t1 相加得到带有位置信息的向量.
如果我们假设嵌入的维度为 4,实际的位置编码将看起来像这样.
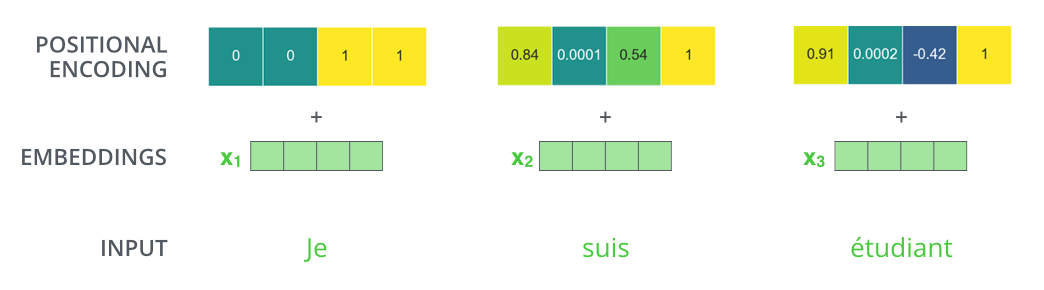
一个具有toy-embedding大小 4 的实际位置编码示例
这可能的图案是什么样的?
在下图中,每一行对应一个向量的位置编码。因此,第一行将是我们要添加到输入序列中第一个词嵌入的向量。
每一行包含 512 个值 - 每个值介于 1 和-1 之间。我们已用颜色编码它们,以便可见模式。
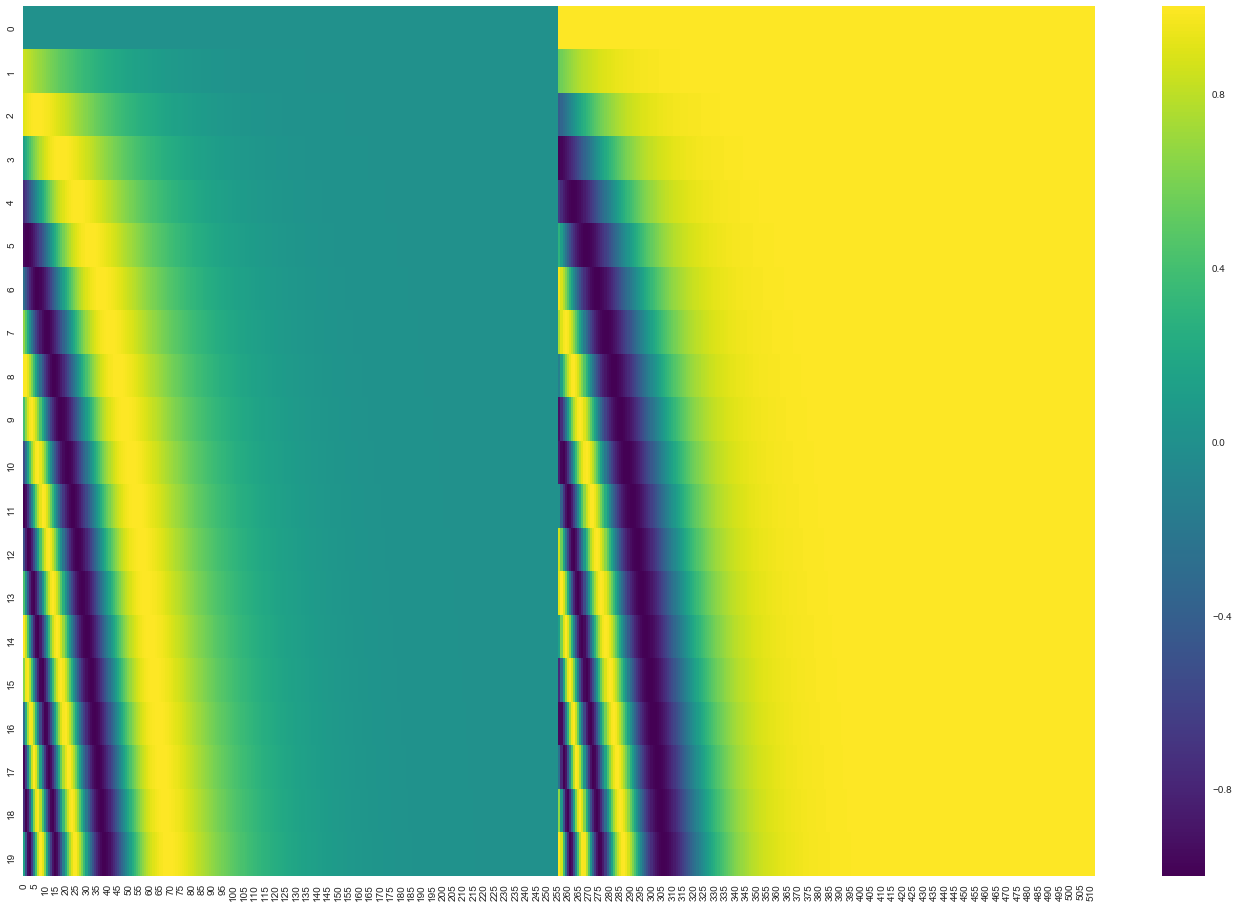
一个具有 512(列)嵌入大小的 20 个单词(行)位置编码的真实示例。您可以看到它从中间分开。这是因为左半部分的值由一个函数(使用正弦)生成,而右半部分的值由另一个函数(使用余弦)生成。然后它们被连接起来形成每个位置编码向量。
位置编码并不是唯一的方法, 当前的图示基于位置编码的公式在论文(第 3.5 节)中描述。您可以在 get_timing_signal_1d() 中看到生成位置编码的代码。它具有能够扩展到未见过的序列长度的优势(例如,如果我们的训练模型被要求翻译比我们训练集中任何句子都长的句子)。
The Residuals (残差)
编码器架构中的一个细节,在继续之前需要提及的是,每个编码器中的每个子层(自注意力、前馈神经网络)周围都有一个残差连接,并且随后是一个层归一化步骤。
下面几点可以帮助理解残差连接在 Transformer 中的作用.
- 跳跃连接的机制
在 Transformer 的每个子层(如自注意力层和前馈神经网络层)中,输入经过层的处理后会与原始输入相加。这个加法操作使得模型在学习时可以“跳过”某些层的非线性变换,从而保持初始输入的信息,确保信息在网络中更稳定地流动。
- 缓解梯度消失和加速收敛
深层网络往往容易出现梯度消失或梯度爆炸的问题,而残差连接通过直接将输入传递到更深的层,帮助梯度在反向传播过程中更顺畅地传递。这不仅减小了梯度消失的风险,还能使模型训练更快、更稳定。
- 模型的表达能力
残差连接允许每一层学习到的是对输入信号的“修正”或“残差”,而不是完全重构整个信号。这种方式使得每一层只需关注输入与输出之间的差异,从而简化了学习任务,提高了模型的表达能力。
- 与归一化的结合
在 Transformer 中,残差连接通常与层归一化(Layer Normalization)结合使用。先进行残差连接,再经过归一化处理,可以进一步稳定训练过程,提升模型性能。
如果我们可视化与自注意力相关的向量和层归一化操作,它看起来会是这样: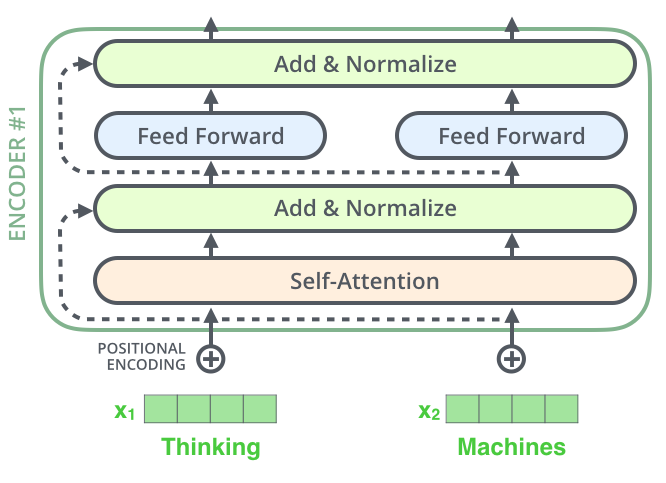
image.png
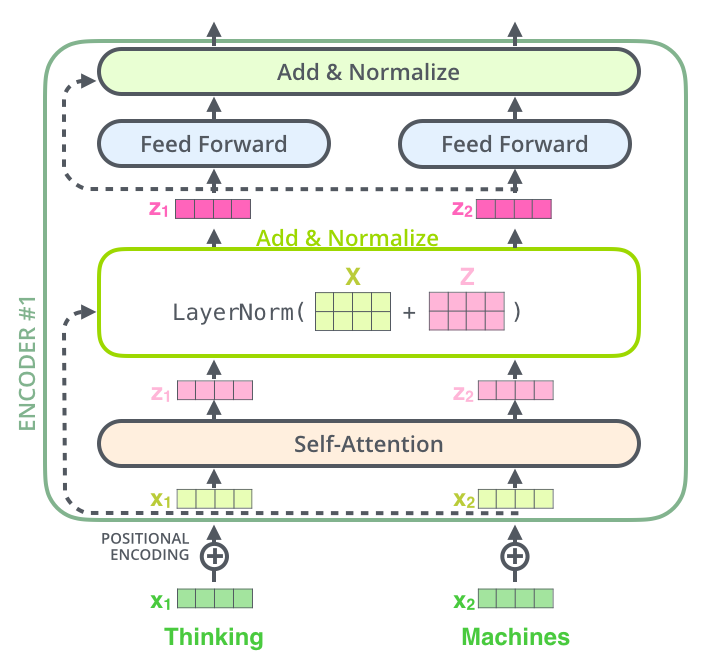
image.png
这同样适用于解码器的子层。如果我们考虑一个由 2 个堆叠的编码器和解码器组成的 Transformer,它看起来会是这样.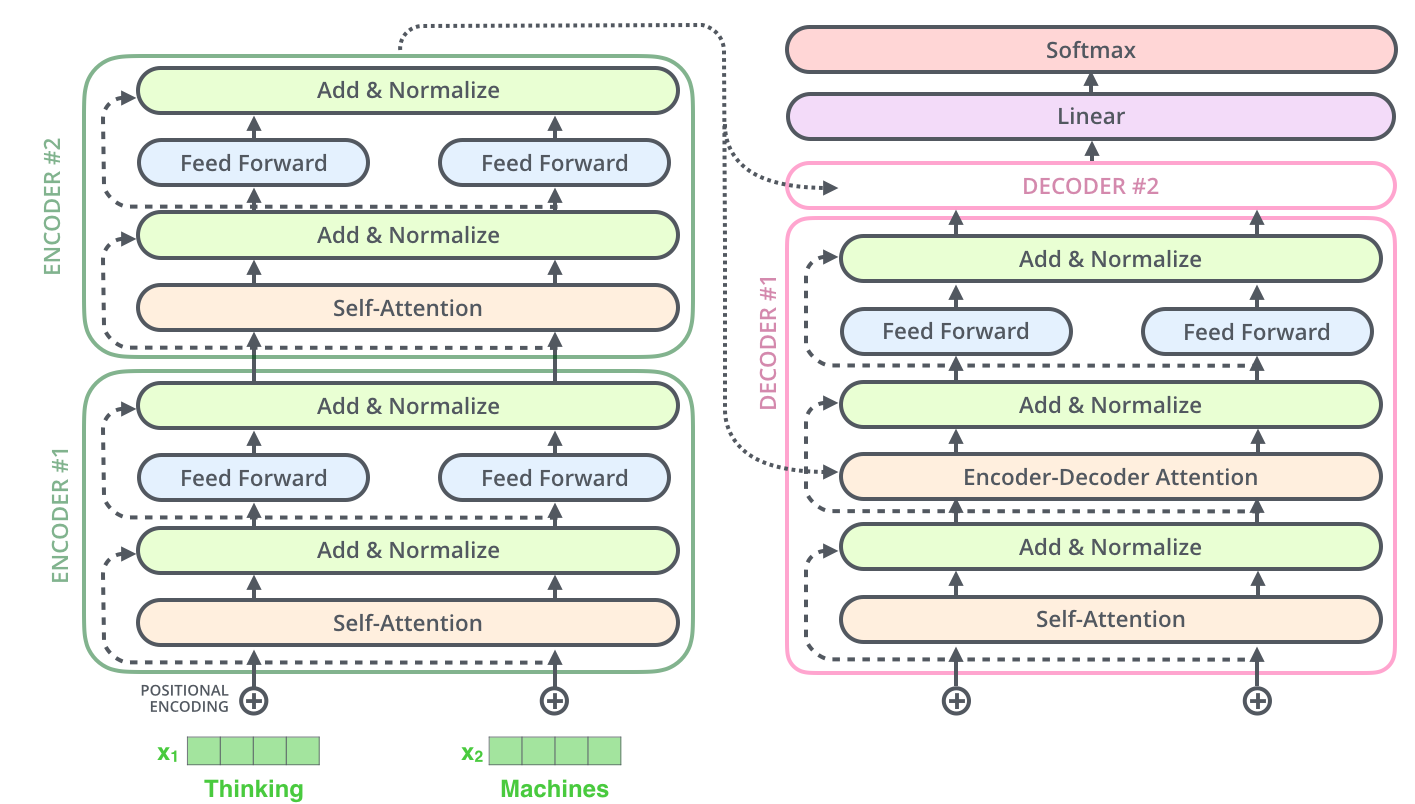
image.png
Decoder 解码器
现在我们已经涵盖了编码器方面的多数概念,我们基本上也知道了解码器组件是如何工作的。但让我们看看它们是如何协同工作的。
编码器首先处理输入序列。然后,顶层编码器的输出被转换为一组注意力向量 Key 和 Value。这些向量将被每个解码器在其“编码器-解码器注意力”层中使用,这有助于解码器关注输入序列中的适当位置:
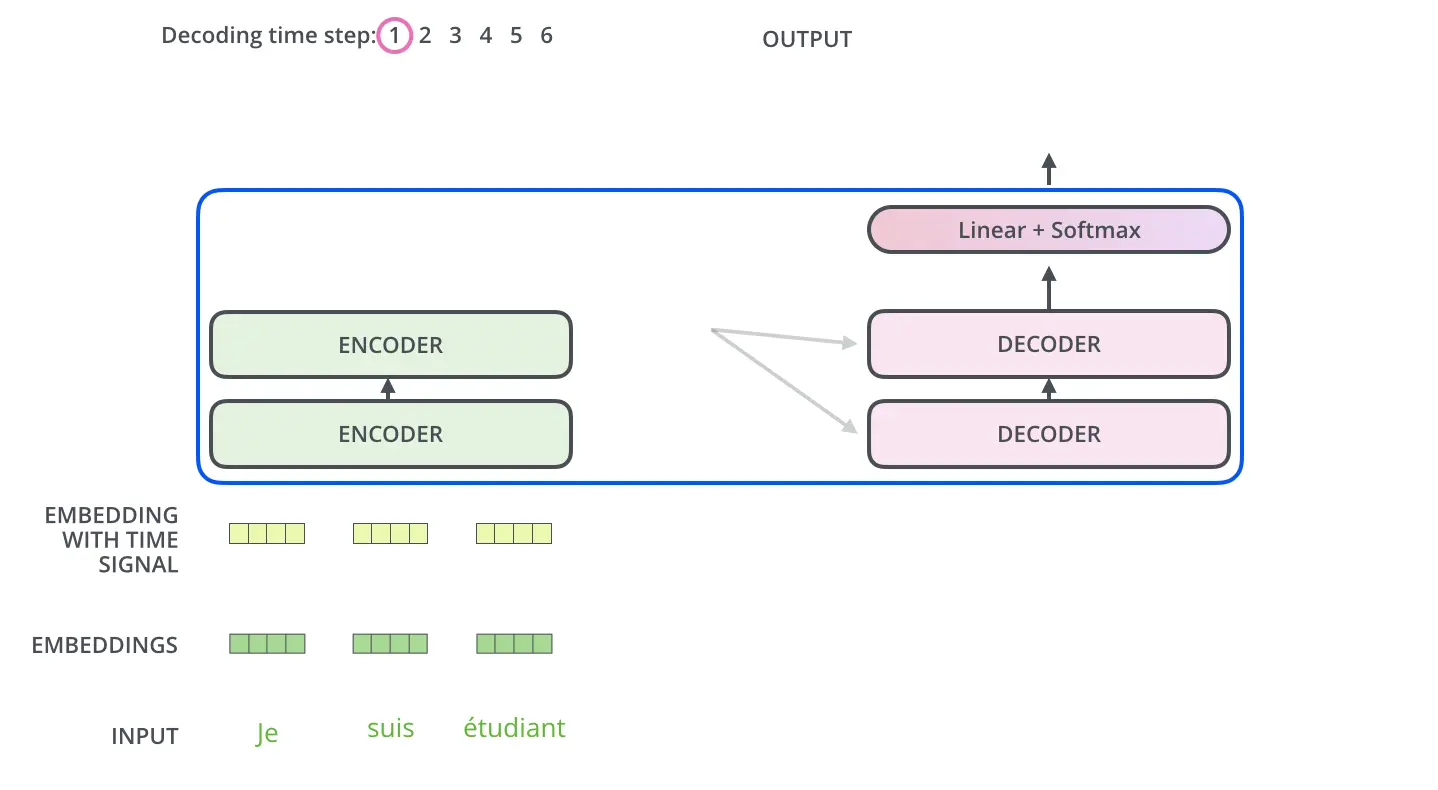
编码阶段完成后,我们开始解码阶段。解码阶段的每一步都会从输出序列(本例中的英文翻译句子)输出一个元素。
以下步骤重复执行,直到达到一个特殊符号,表示变压器解码器已完成输出。
每一步的输出被馈送到下一个时间步的底部解码器,解码器像编码器一样冒泡式地上升其解码结果。就像我们对编码器输入所做的那样,我们将嵌入和添加位置编码到这些解码器输入中,以指示每个单词的位置。
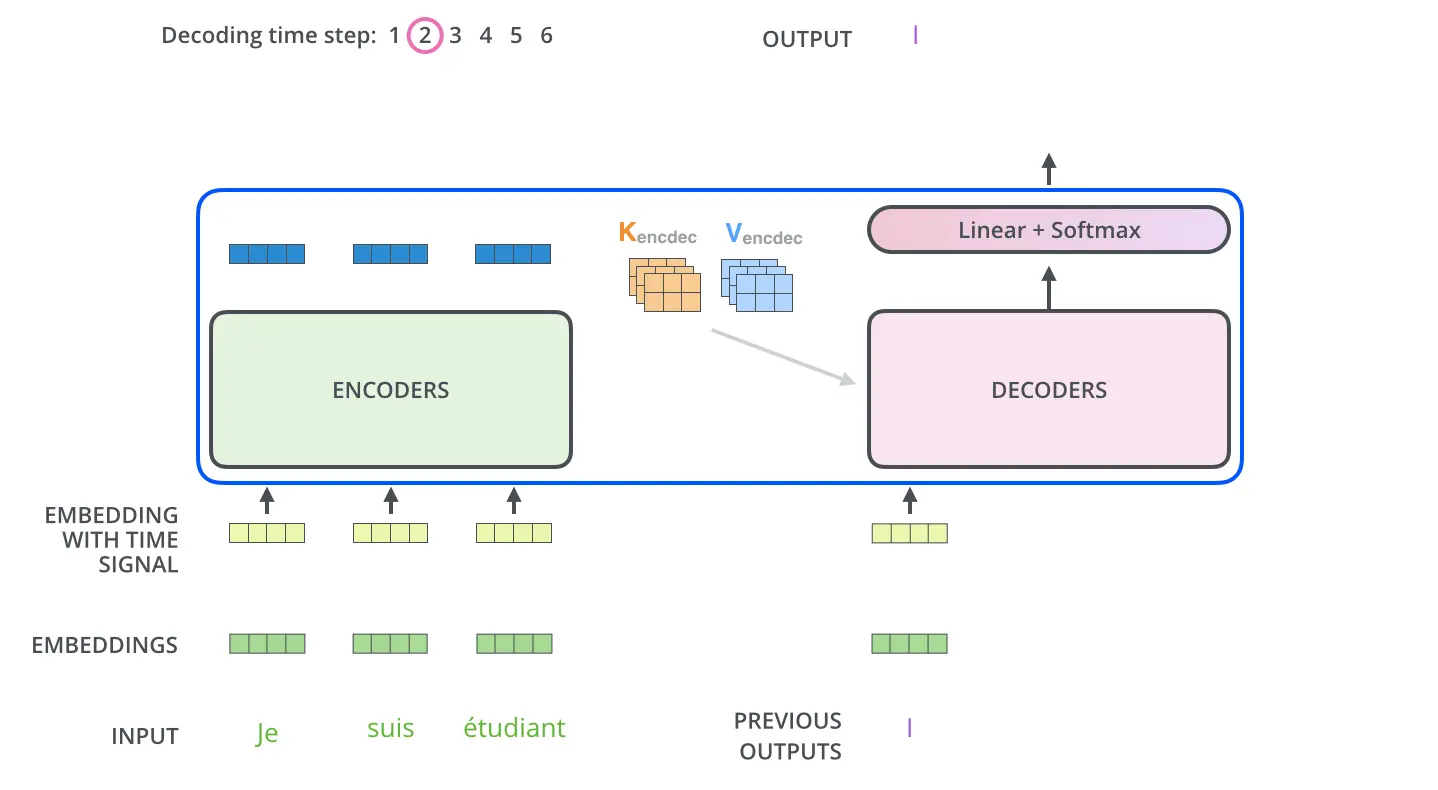
图解
解码器中的自注意力层以略不同于编码器中的方式运行.
在解码器中,自注意力层只允许关注输出序列中的较早位置。这是通过在自注意力计算中的 softmax 步骤之前对未来的位置进行Masked掩码(将它们设置为 -inf )来实现的。
The Final Linear and Softmax Layer (最终线性层和 Softmax 层)
解码器堆栈输出一个浮点向量。我们如何将其转换为单词?这是最终线性层的任务,随后是 Softmax 层。
线性层是一个简单的全连接神经网络,它将解码器堆栈产生的向量投影到一个称为 logits 向量的更大向量中。
我们假设我们的模型知道 10,000 个独特的英语单词(我们模型的“输出词汇表”),这些单词是从其训练数据集中学习的。
这将使 logits 向量有 10,000 个单元格宽——每个单元格对应一个独特单词的分数。这就是我们解释模型输出后跟线性层输出的方式。
softmax 层随后将这些分数转换为概率(所有都是正数,总和为 1.0)。选择概率最高的单元格,并输出与其关联的单词作为当前的输出。
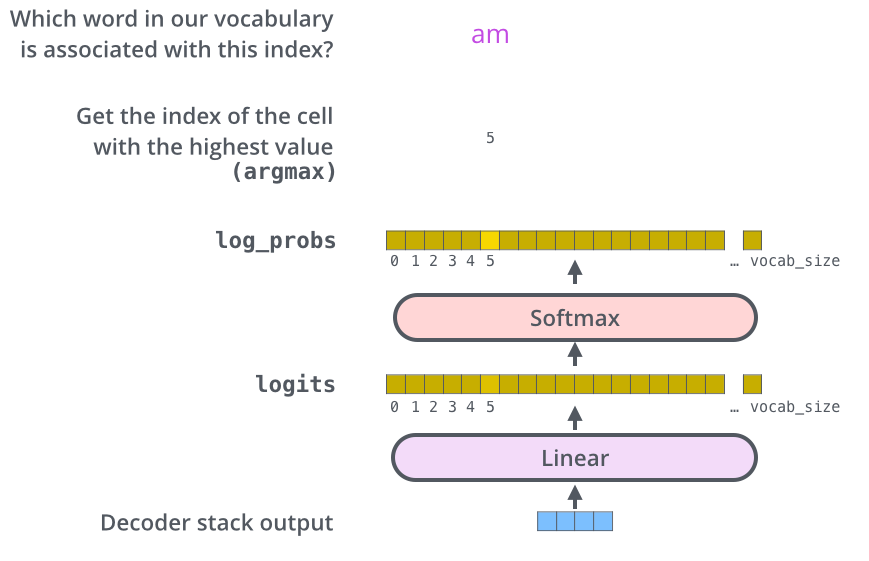
此图从底部开始,以解码器堆栈的输出向量作为起点。然后将其转换为输出词
The Loss Function 损失函数
假设我们正在训练我们的模型。假设这是训练阶段的第一步,我们在一个简单的例子上训练它——将“merci”翻译成“谢谢”。
这意味着我们希望输出是一个表示“谢谢”这个单词的概率分布。但由于这个模型尚未训练,这种情况短期内不太可能发生。
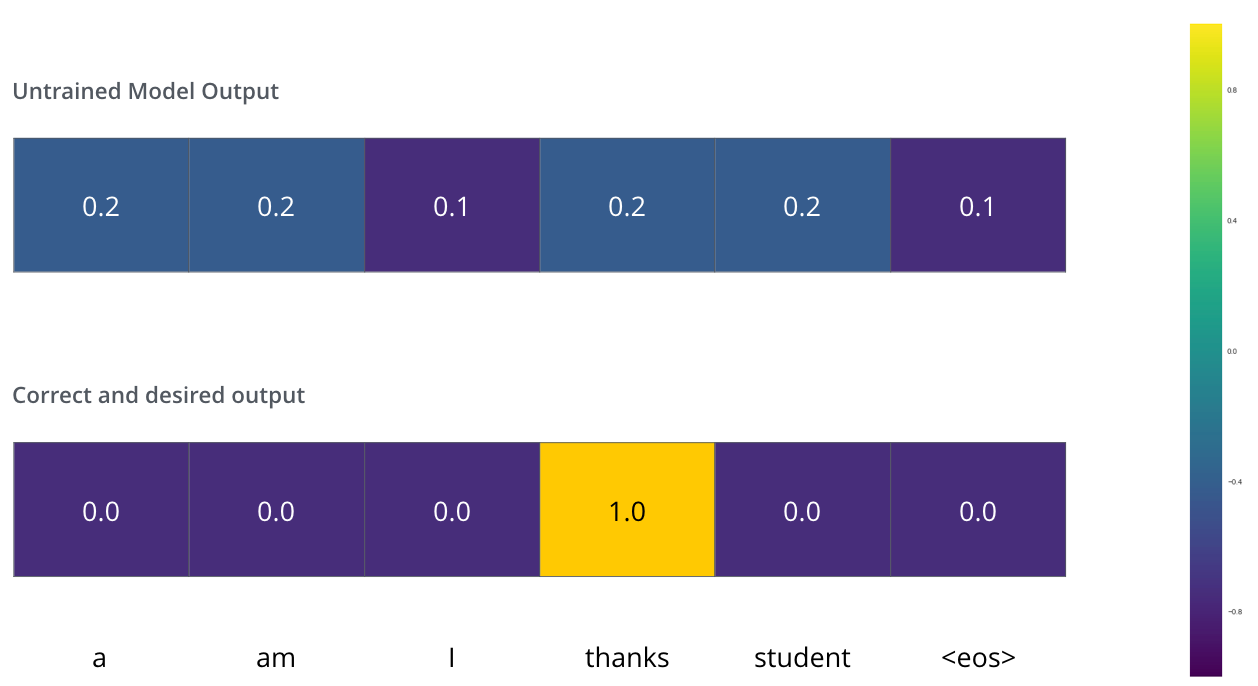
模型参数(权重)全部随机初始化,因此(未训练)的模型为每个单元格/单词生成具有任意值的概率分布。我们可以将其与实际输出进行比较,然后通过反向传播调整所有模型权重,使输出更接近期望输出。
如何比较两个概率分布?我们只需将一个从另一个中减去。更多详情,请查看cross-entropy和 Kullback–Leibler divergence。
但是请注意,这是一个过于简化的例子。更现实的情况是,我们将使用一个超过一个单词的句子。例如——输入:“je suis étudiant”和预期输出:“我是学生”。这实际上意味着我们希望我们的模型连续输出概率分布,其中.
- 每个概率分布由一个宽度为 vocab_size 的向量表示(在我们的示例中为 6,但更现实的是 30,000 或 50,000 这样的数字)
- 第一个概率分布的最高概率在“i”这个词对应的单元格上
- 第二个概率分布的最高概率出现在与单词“am”相关的单元格中
- 如此等等,直到第五个输出分布指示“
<end of sentence>”符号,该符号也与其关联的来自 10,000 个元素词汇表中的单元格相关。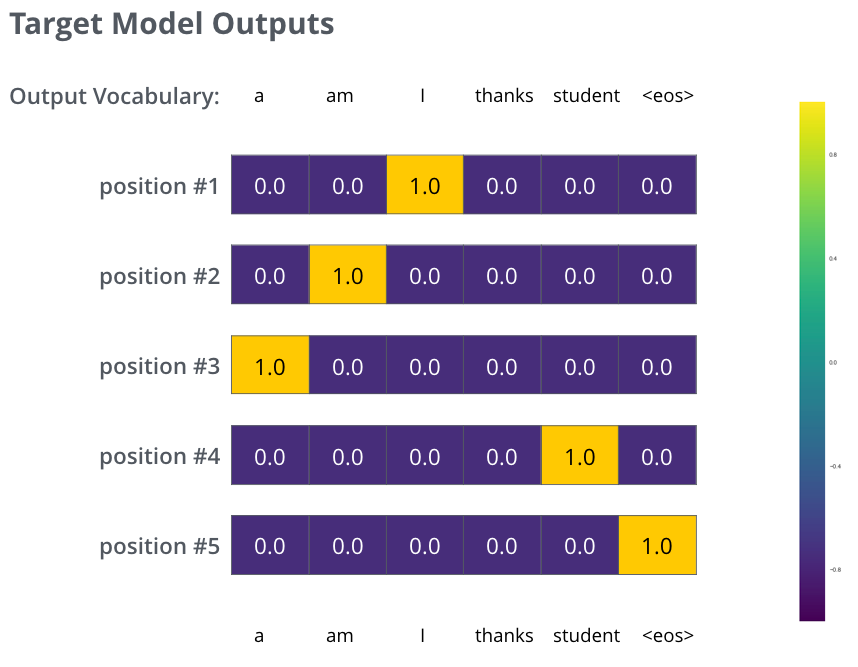
image.png
在足够大的数据集上训练模型足够长的时间后,我们希望产生的概率分布看起来像这样: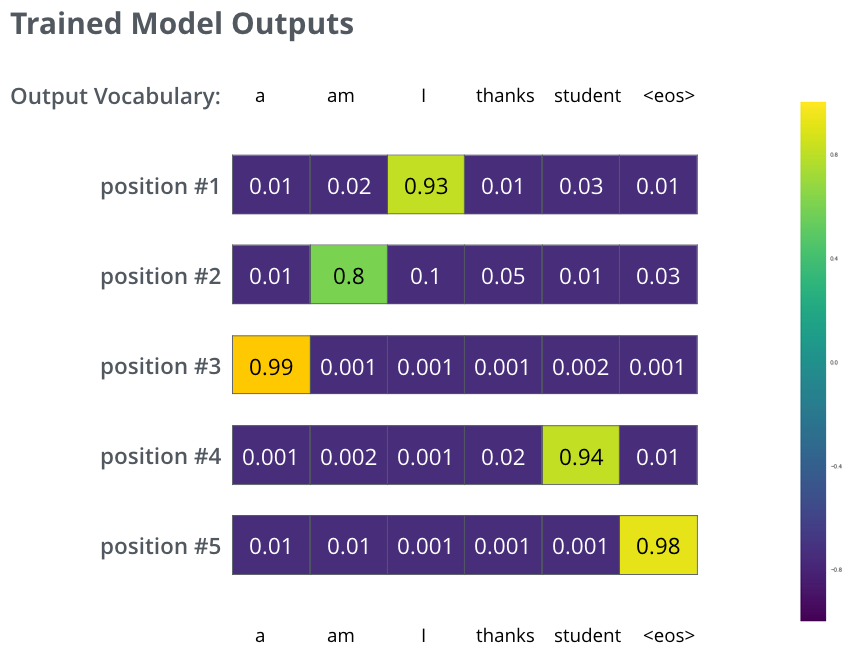
image.png
现在,由于模型一次生成一个输出,我们可以假设模型正在从该概率分布中选择概率最高的单词,并丢弃其余的。这是其中一种方法(称为贪婪解码)。
另一种方法是保留,比如说,前两个单词(例如,'我'和'a'),然后在下一步中运行模型两次:一次假设第一个输出位置是单词'我',另一次假设第一个输出位置是单词'a',然后保留考虑位置#1 和#2 产生较少错误的版本。我们对位置#2 和#3 等重复此操作。这种方法称为“beam search(束搜索)”,在我们的例子中,bean大小为两个(意味着在所有时候,内存中保留两个部分假设(未完成的翻译)),top_beams 也为两个(意味着我们将返回两个翻译)。