Implement a GPT model 2.Normalizing activations with layer normalization
训练深度神经网络时,由于梯度消失或爆炸等问题,有时会面临挑战。这些问题导致训练动态不稳定,使得网络难以有效调整其权重,这意味着学习过程难以找到一组参 数(权重),使神经网络的损失函数最小化。换句话说,网络在学习数据中的潜在模 式方面存在困难,这使得它难以进行准确的预测或决策。
现在让我们实现 layer normalization 以提高神经网络训练的稳定性和效率。层归一化的主要思想是调整神经网络层的激活(输出),使其均值为 0,方差为 1,也称为单位方差。这种调整加快了模型收敛到有效权重的速度,并确保了一致可靠的训练。
均值和方差
在 GPT-2 和现代变换器架构中,层归一化通常在多头注意力模块之前和之后应用.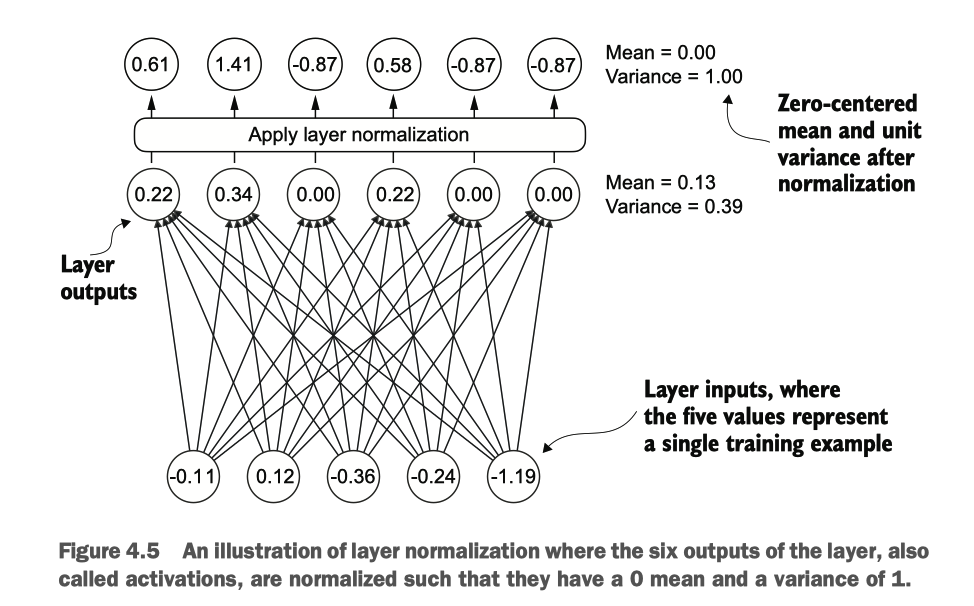
层归一化的示意图,其中层的六个输出,也被称为激活,被归一化,使其具有 0 的 均值和 1 的方差。
torch.manual_seed(123)
# create 2 training examples with 5 dimensions (features) each
batch_example = torch.randn(2, 5)
layer = nn.Sequential(nn.Linear(5, 6), nn.ReLU())
out = layer(batch_example)
print(out)
## output
tensor([[0.2260, 0.3470, 0.0000, 0.2216, 0.0000, 0.0000],
[0.2133, 0.2394, 0.0000, 0.5198, 0.3297, 0.0000]],
grad_fn=<ReluBackward0>)
我们编码的神经网络层由一个线性层和一个非线性激活函数ReLU(整流线性单元的简称)组成,这是一种神经网络中标准的激活函数。如果你对ReLU不熟悉,它简单地将负输入阈值化为0,确保层输出仅为正值,这也解释了为什么结果层的输出不包含任何负值。
在我们对这些输出应用层归一化之前,让我们查看一下均值和方差:
mean = out.mean(dim=-1, keepdim=True)
var = out.var(dim=-1, keepdim=True)
print("Mean:\n", mean)
print("Variance:\n", var)
## output
Mean:
tensor([[0.1324], # 第一行tensor均值
[0.2170]], grad_fn=<MeanBackward1>) # 第二行tensor均值
Variance:
tensor([[0.0231],
[0.0398]], grad_fn=<VarBackward0>)
Tensor 维度保持
在进行均值或方差计算等操作时使用 keepdim=True,可以确保输出张量保留与输入 张量相同的维度数量,即使该操作沿着通过 dim 指定的维度减少了张量。例如,如果 不使用 keepdim=True,返回的均值张量将是一个二维向量 [0.1324, 0.2170],而不是一 个 2 × 1 维的矩阵 [[0.1324], [0.2170]]。
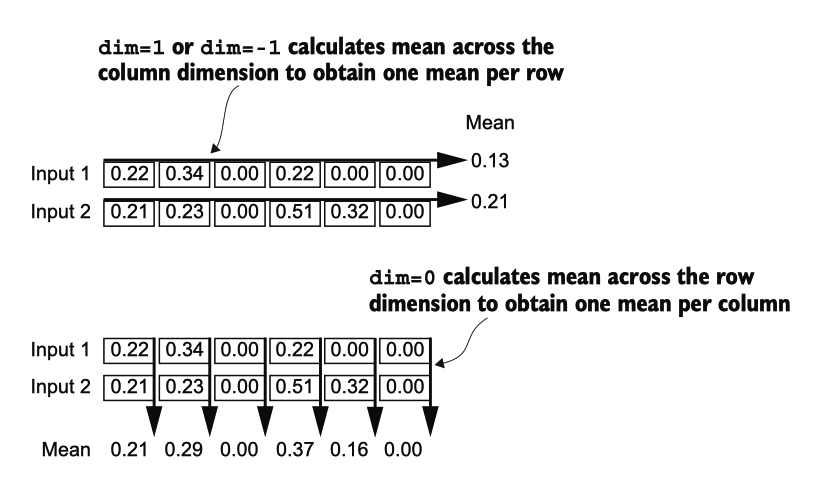
An illustration of the dim parameter when calculating the mean of a tensor.
例如,如果我们有一个维度为 [行, 列] 的二维张量(矩阵),使用 dim=0 将在行之间(垂直,如底部所示)执行操作 ,生成的输出将聚合每列的数据。使用 dim=1 或 dim=-1 将在列之间(水平方 向,如顶部所示)执行操作,生成的输出将聚合每行的数据。
一个二维张量(类似于矩阵),使用 dim=-1 进行均值或方差计算的操作与使用 dim=1 是一样的。这是因为 -1 指的是张量的最后一个维度,它对应于二维张量中的列。稍后 ,在 GPT 模型中添加层归一化时,该模型产生形状为 [batchsize, numtokens, embedd ing_size] 的三维张量,我们仍然可以使用 dim=-1 进行最后维度的归一化,避免从 dim=1 变为 dim=2。
Layer Normalization 层归一化
接下来,让我们对之前获得的层输出应用层归一化。该操作包括减去均值并除以方 差的平方根(也称为标准差):
out_norm = (out - mean) / torch.sqrt(var)
print("Normalized layer outputs:\n", out_norm)
mean = out_norm.mean(dim=-1, keepdim=True)
var = out_norm.var(dim=-1, keepdim=True)
print("Mean:\n", mean)
print("Variance:\n", var)
## output
Normalized layer outputs:
tensor([[ 0.6159, 1.4126, -0.8719, 0.5872, -0.8719, -0.8719],
[-0.0189, 0.1121, -1.0876, 1.5173, 0.5647, -1.0876]],
grad_fn=<DivBackward0>)
Mean:
tensor([[-5.9605e-08],
[ 1.9868e-08]], grad_fn=<MeanBackward1>)
Variance:
tensor([[1.0000],
[1.0000]], grad_fn=<VarBackward0>)
请注意,输出张量中的值 –5.9605e-08 是 –5.9605 × 10 -8 的科学记数法,十进制形式 为 –0.000000059605。该值非常接近于 0,但由于计算机表示数字时有限精度导致的 小数误差,它并不完全等于 0。
为了提高可读性,我们还可以通过将 sci_mode 设置为 False 来关闭打印张量值时的科学计数法:
torch.set_printoptions(sci_mode=False)
print("Mean:\n", mean)
print("Variance:\n", var)
Mean:
tensor([[ -0.0000],
[ 0.0000]], grad_fn=<MeanBackward1>)
Variance:
tensor([[1.0000],
[1.0000]], grad_fn=<VarBackward0>)
到目前为止,我们已经逐步编码并应用了层规范化。现在,让我们将这个过程封装到 一个可以在后面的GPT模型中使用的PyTorch模块中。
应用Layer Normalization
class LayerNorm(nn.Module):
def __init__(self, emb_dim):
super().__init__()
self.eps = 1e-5
self.scale = nn.Parameter(torch.ones(emb_dim))
self.shift = nn.Parameter(torch.zeros(emb_dim))
def forward(self, x):
mean = x.mean(dim=-1, keepdim=True)
var = x.var(dim=-1, keepdim=True, unbiased=False)
norm_x = (x - mean) / torch.sqrt(var + self.eps)
return self.scale * norm_x + self.shift
- 该特定的层归一化实现作用于输入张量 x 的最后一个维度,该维度表示嵌入维度 (emb_dim)。
- 变量 eps 是一个小常数 (epsilon),它被添加到方差中以防止在归一化过程中出现零除法。
- scale和shift是两个可训练参数(与输入具有相同的维度),如果确定这样 做可以提高模型在其训练任务上的性能,则 LLM 会在训练过程中自动调整它们。这使得模型能够学习适当的缩放和偏移,以最适合其处理的数据。
[!NOTE] 偏差方差
在我们的方差计算方法中,我们通过设置 unbiased=False 使用了一个实现细节。对于 那些好奇这意味着什么的人,在方差计算中,我们在方差公式中将总数除以输入的 数量 n。这种方法不适用于贝塞尔修正,贝塞尔修正通常在分母中使用 n – 1 而不 是 n 来调整样本方差估计的偏差。这个决定导致了所谓的方差偏差估计。对于嵌入 维度 n 显著较大的 LLM 来说,使用 n 和 n –1 之间的差异实际上是微不足道的。我 选择这种方法是为了确保与 GPT-2 模型的归一化层兼容,并且因为它反映了 TensorF low 的默认行为,这种行为用于实现原始的 GPT-2 模型。使用类似的设置确保我们的方法与后续加载的预训练权重兼容。
现在让我们在实践中尝试 LayerNorm 模块并将其应用于批输入:
ln = LayerNorm(emb_dim=5)
out_ln = ln(batch_example)
mean = out_ln.mean(dim=-1, keepdim=True)
var = out_ln.var(dim=-1, unbiased=False, keepdim=True)
print("Mean:\n", mean)
print("Variance:\n", var)
## output
Mean:
tensor([[ -0.0000],
[ 0.0000]], grad_fn=<MeanBackward1>)
Variance:
tensor([[1.0000],
[1.0000]], grad_fn=<VarBackward0>)
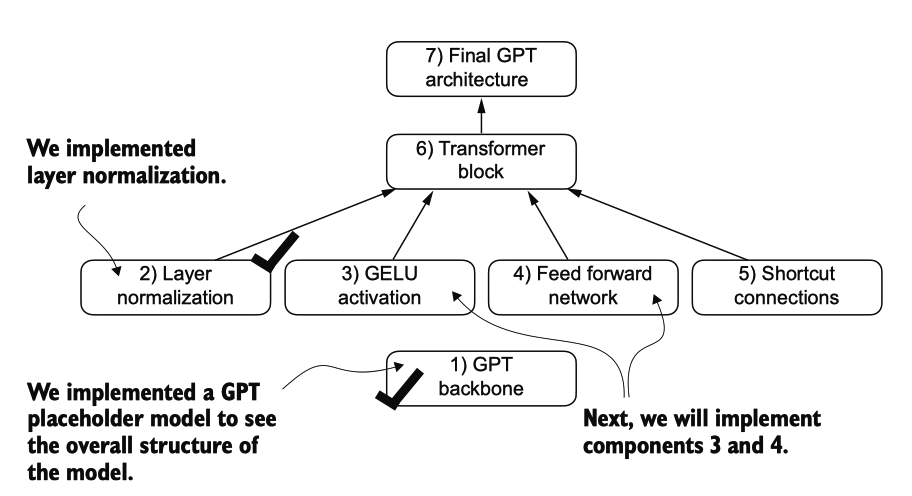
The building blocks necessary to build the GPT architecture. So far, we have completed the GPT backbone and layer normalization. Next, we will focus on GELU activation and the feed forward network.