Implement a GPT model 4. Shortcut Connections & Transformer Block
Shortcut Connections
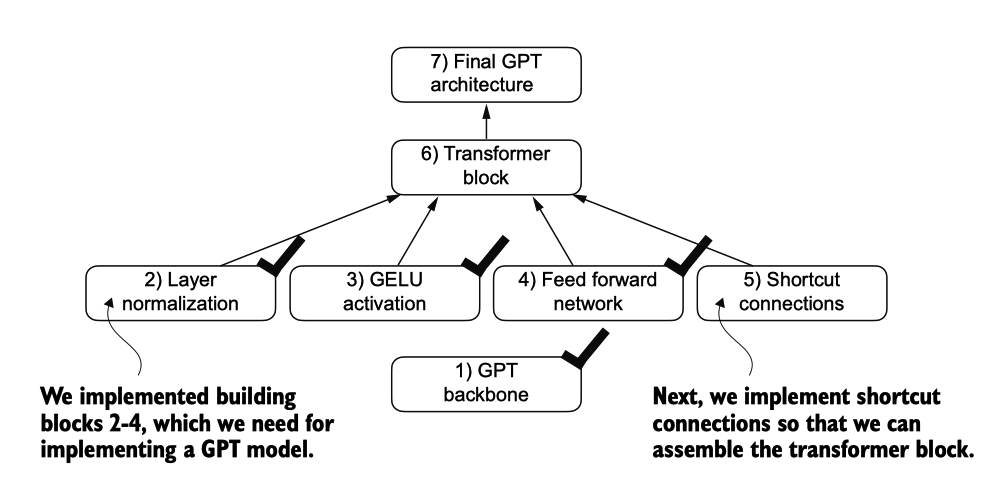
Next Build
让我们讨论一下shortcut connections背后的概念,也称为跳跃连接或残差连接。
最初,短路连接是为了解决计算机视觉中的深度网络(特别是残差网络)而提出的,以减轻消失梯度问题。
消失梯度问题是指在通过层向后传播时,梯度(指导训练期间的权重 更新)逐渐变小,这使得有效训练早期层变得困难。
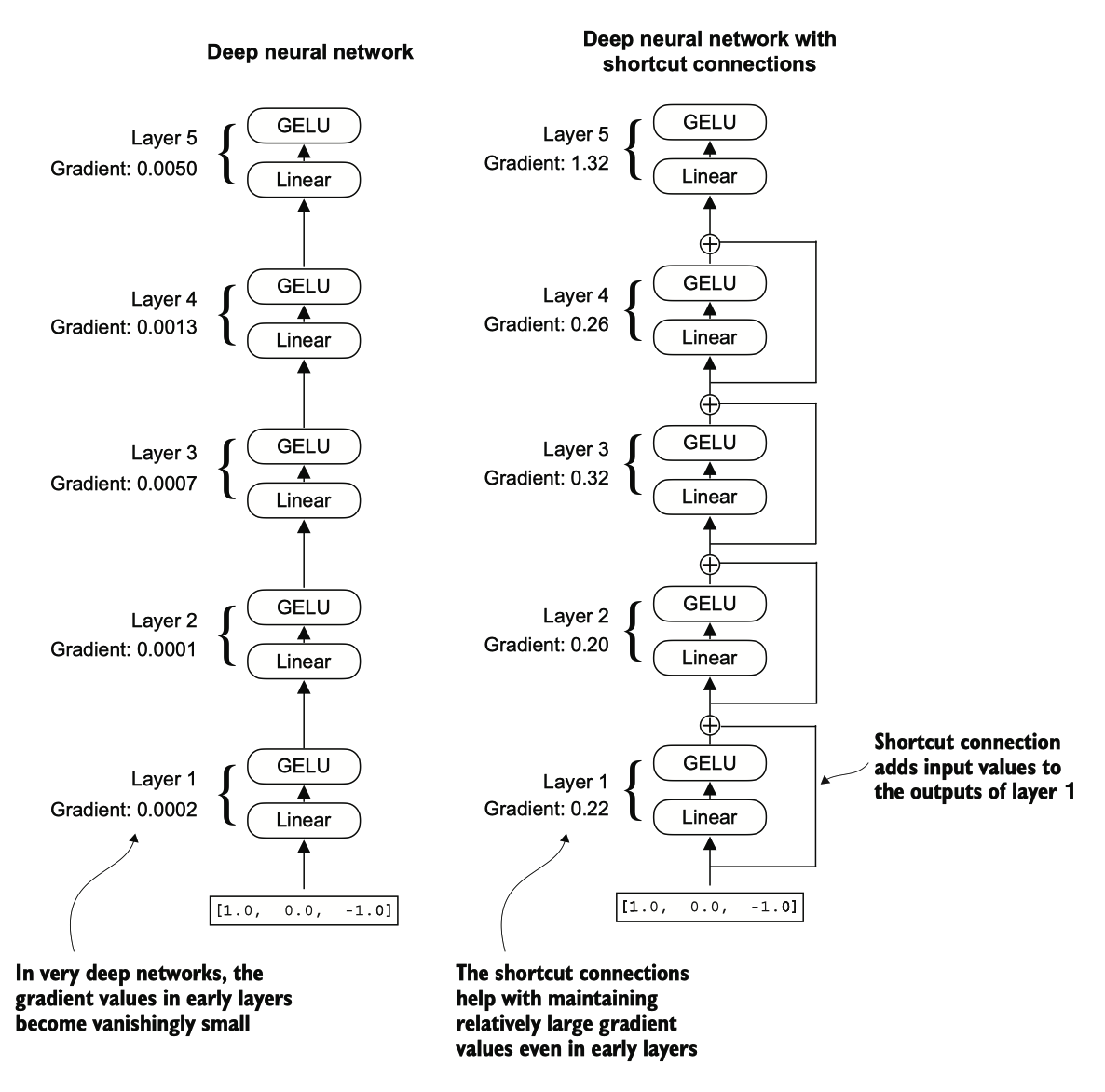
图 4.12 组成五层的深度神经网络的比较,左侧为没有跳跃连接,右侧为有跳跃连接。
图 4.12 显示了一个快捷连接通过跳过一层或多层为梯度在网络中流动创建了一个替代的、更短的路径,这通过将一层的输出添加到后面一层的输出来实现。这就是为什么这些连接也被称为跳跃连接。它们在训练中的向后传播过程中对于保持梯度流动起着关键作用。
跳跃连接涉及将一层的输入 添加到其输出中,实际上创建了一个绕过某些层的替代路径。梯度表示每一层的平均绝对梯度
class ExampleDeepNeuralNetwork(nn.Module):
def __init__(self, layer_sizes, use_shortcut):
super().__init__()
self.use_shortcut = use_shortcut
self.layers = nn.ModuleList([
nn.Sequential(nn.Linear(layer_sizes[0], layer_sizes[1]), GELU()),
nn.Sequential(nn.Linear(layer_sizes[1], layer_sizes[2]), GELU()),
nn.Sequential(nn.Linear(layer_sizes[2], layer_sizes[3]), GELU()),
nn.Sequential(nn.Linear(layer_sizes[3], layer_sizes[4]), GELU()),
nn.Sequential(nn.Linear(layer_sizes[4], layer_sizes[5]), GELU())
])
def forward(self, x):
for layer in self.layers:
# Compute the output of the current layer
layer_output = layer(x)
# Check if shortcut can be applied
if self.use_shortcut and x.shape == layer_output.shape:
x = x + layer_output
else:
x = layer_output
return x
def print_gradients(model, x):
# Forward pass
output = model(x)
target = torch.tensor([[0.]])
# Calculate loss based on how close the target
# and output are
loss = nn.MSELoss()
loss = loss(output, target)
# Backward pass to calculate the gradients
loss.backward()
for name, param in model.named_parameters():
if 'weight' in name:
# Print the mean absolute gradient of the weights
print(f"{name} has gradient mean of {param.grad.abs().mean().item()}")
该代码实现了一个具有五层的深度神经网络,每层由一个线性层和一个GELU激活函 数组成。在前向传递中,我们通过层迭代地传递输入,并在self.use_shortcut属性设 为True时可选择添加Shortcut Connection。
让我们使用这段代码来初始化一个没有Shortcut Connection的神经网络。每一层将被初始化为 接受具有三个输入值的示例并返回三个输出值。最后一层返回一个输出值:
layer_sizes = [3, 3, 3, 3, 3, 1]
sample_input = torch.tensor([[1., 0., -1.]])
torch.manual_seed(123)
model_without_shortcut = ExampleDeepNeuralNetwork(
layer_sizes, use_shortcut=False
)
print_gradients(model_without_shortcut, sample_input)
## output
layers.0.0.weight has gradient mean of 0.00020173587836325169
layers.1.0.weight has gradient mean of 0.00012011159560643137
layers.2.0.weight has gradient mean of 0.0007152039906941354
layers.3.0.weight has gradient mean of 0.0013988736318424344
layers.4.0.weight has gradient mean of 0.005049645435065031
此代码指定了一个损失函数,用于计算模型输出与用户指定目标(这里为了简单起见 ,目标值为0)之间的接近程度。然后,当调用 loss.backward() 时,PyTorch 将计算模型中每一层的损失梯度。我们可以通过 model.named_parameters() 迭代权重参数。假设 我们对于给定层有一个 3 × 3 权重参数矩阵。在这种情况下,该层将具有 3 × 3 梯度值 ,我们打印这 3 × 3 梯度值的平均绝对梯度,以获得每层的单一梯度值,从而更容易比较层之间的梯度。
简而言之,.backward() 方法是 PyTorch 中一个方便的方法,它计算损失梯度,这在模型训练中是必需的,而无需我们自己实现梯度计算的数学,因此使得处理深度神经网络变得更加可及。
print_gradients 函数的输出显示,随着从最后一层(layers.4)到第一层(layers.0)的 推进,梯度变得越来越小,这是一种称为 vanishing gradient problem 的现象。
现在让我们实例化一个具有跳过连接的模型,并看看它的表现如何:
torch.manual_seed(123)
model_with_shortcut = ExampleDeepNeuralNetwork(
layer_sizes, use_shortcut=True
)
print_gradients(model_with_shortcut, sample_input)
## output
layers.0.0.weight has gradient mean of 0.22169792652130127
layers.1.0.weight has gradient mean of 0.20694106817245483
layers.2.0.weight has gradient mean of 0.32896995544433594
layers.3.0.weight has gradient mean of 0.2665732204914093
layers.4.0.weight has gradient mean of 1.3258540630340576
最后一层 (layers.4) 的梯度仍然大于其他层。然而,随着我们向第一层 (layers.0) 进展 ,梯度值稳定下来,并且并没有缩小到一个微不足道的值。
总之,Shortcut Conenctions对于克服深度神经网络中梯度消失问题所带来的限制非常重要。快 捷连接是非常大模型(如LLMs)的核心构建块,它们将有助于通过确保在训练下一章中的GPT模型时各层之间保持一致的梯度流,从而促进更有效的训练。
接下来,我们将把之前涉及的所有概念(层归一化、GELU 激活、FeedForward和Shortcut Connection)连接在一起,形成一个TransformerBlock,这是我们编码 GPT 架构所需的最终构建块。
Transformer Block
现在,让我们实现 transformer block,这是 GPT 和其他 LLM 架构的一个基本构建块。
这个块在参数为 1.24 亿的 GPT-2 架构中重复了十几次,结合了我们之前覆盖的几个概 念:多头注意力、层归一化、丢弃、前馈层和 GELU 激活。稍后,我们将把这个Transformer Block与 GPT 架构的其余部分连接起来。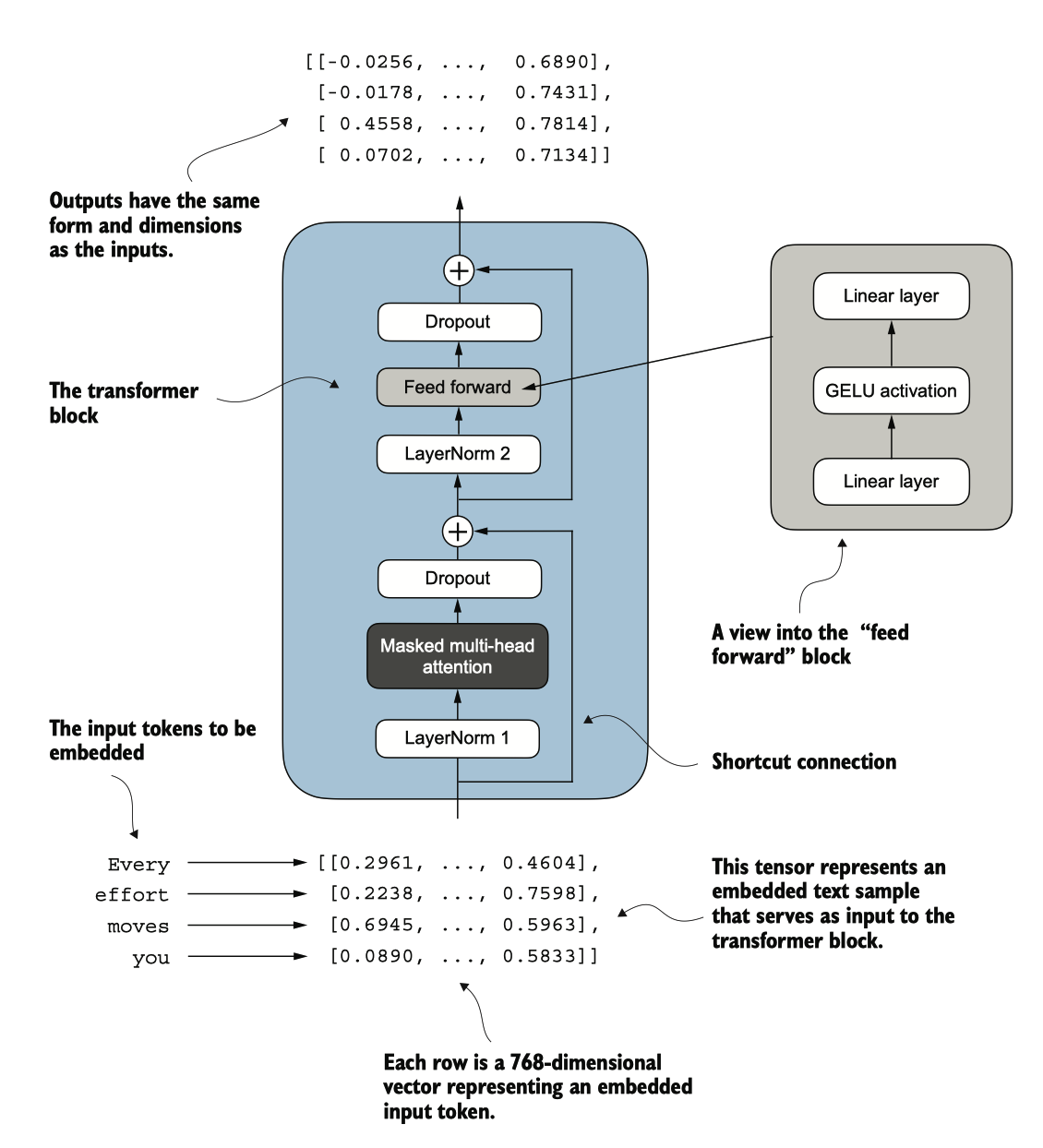
图 4.13 一个Transformer Block的示例。输入标记已被嵌入到 768 维向量中。每一行对应一个标记的向量表示 。Transformer Block的输出是与输入相同维度的向量,这些向量可以被输入到 LLM 的后续层中。
图 4.13 显示了一个Transformer模块,该模块结合了多个组件,包括Masked Multi-head Attention Module和我们之前实现的FeedForward模)。当Transformer模块处理输入序列时,序列中的每个元素(例如,一个词或子词标记)由一个固定大小的向量 表示(在这种情况下为768维度)。Transformer模块内部的操作,包括Multi-head Attention和FeedForward层,旨在以保持这些向量维度的方式对其进行转换。
这个想法是,Masked Multi-head Attention Module中的自注意力机制识别并分析输入序列中元素之间的关系。相反,FeedForward Network在每个位置上单独修改数据。这种组合不仅使输入能够更细致地理解和处理,还增强了模型处理复杂数据模式的整体能力。
from previous_chapters import MultiHeadAttention
class TransformerBlock(nn.Module):
def __init__(self, cfg):
super().__init__()
self.att = MultiHeadAttention(
d_in=cfg["emb_dim"],
d_out=cfg["emb_dim"],
context_length=cfg["context_length"],
num_heads=cfg["n_heads"],
dropout=cfg["drop_rate"],
qkv_bias=cfg["qkv_bias"])
self.ff = FeedForward(cfg)
self.norm1 = LayerNorm(cfg["emb_dim"])
self.norm2 = LayerNorm(cfg["emb_dim"])
self.drop_shortcut = nn.Dropout(cfg["drop_rate"])
def forward(self, x):
# Shortcut connection for attention block
shortcut = x
x = self.norm1(x)
x = self.att(x) # Shape [batch_size, num_tokens, emb_size]
x = self.drop_shortcut(x)
x = x + shortcut # Add the original input back
# Shortcut connection for feed forward block
shortcut = x
x = self.norm2(x)
x = self.ff(x)
x = self.drop_shortcut(x)
x = x + shortcut # Add the original input back
return x
给定的代码在 PyTorch 中定义了一个 TransformerBlock 类,其中包含多头注意力机制 ( MultiHeadAttention) 和一个前馈网络 (Feed-Forward),这两者都是基于提供的配置字典 (cfg) 进行配置的,例如 GPTCONFIG124M。
层归一化(LayerNorm)在这两个组件之前应用,而 dropout 在它们之后应用以正则化模型并防止过拟合。这也被称为 Pre-LayerNorm。较旧的架构,如原始的 transformer 模型,则在自注意力和Feedforward Network之后应用层归一化,这被称为 Post-LayerNorm,通常会导致更差的训练动态。
该类还实现了FeedFroward,其中每个组件后面都有一个Shortcut Connections,将块的输入添加到其输出中。这一关键特性有助于梯度在训练过程中的流动,并改善深度模型的学习.
使用我们之前定义的 GPTCONFIG124M 字典,让我们实例化一个Transformer Block,并 给它一些示例数据:
torch.manual_seed(123)
x = torch.rand(2, 4, 768) # Shape: [batch_size, num_tokens, emb_dim]
block = TransformerBlock(GPT_CONFIG_124M)
output = block(x)
print("Input shape:", x.shape)
print("Output shape:", output.shape)
## output
Input shape: torch.Size([2, 4, 768])
Output shape: torch.Size([2, 4, 768])
正如我们所看到的,Transformer Block在其输出中保持输入维度,这表明Transformer Block架构在整个网络中处理数据序列而不改变其形状。
在Transformer Block架构中,形状的保持并非偶然,而是其设计的关键方面。这种设计使得它能够有效应用于各种序列到序列的任务,其中每个输出向量直接对应于一个输入向量,保持一对一的关系。然而,输出是一个上下文向量,它封装了来自整个输入序列的信息(。这意味着尽管序列的物理维度(长度和特征大小)在经过Transformer Block时保持不变,但每个输出向量的内容被重新编码,以整合来自整个输入序列的上下文信息。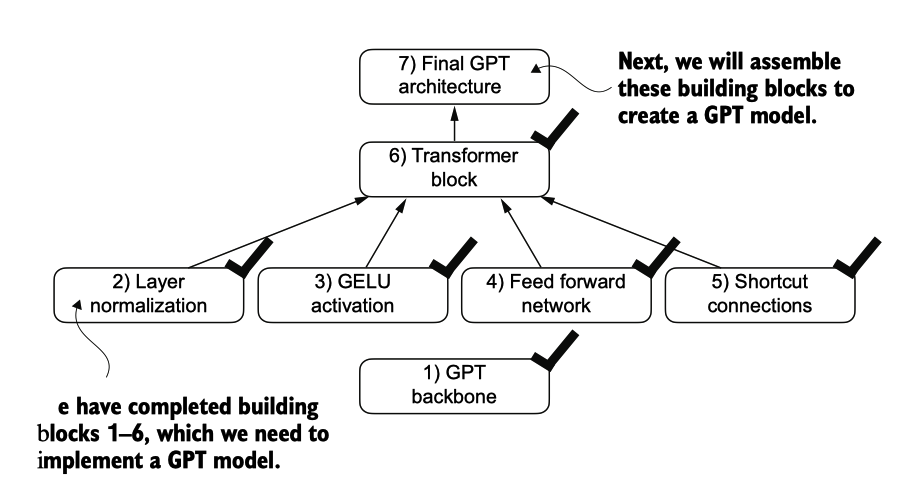
图4.14 构建GPT架构所需的构建模块。黑色勾选表示我们已完成的模块。